Nach langer Rechnerei und der Anwendung der Regeln für komplexe Zahlen habe ich das richtige Ergebnis für den Strom (15,2 mA)rausbekommen.
Irgendwie ist das alles mehr Mathematik als Elektronik habe ich das Gefühl...

@ xeraniad: Die Bilder sind leider nicht lesbar, da zu klein.

Ja, die Bilder waren nur Daumennägel .
Wien-Robinson -Brücke: hier.
LC-Netzwerk: Guck. Der Taschenrechner sagt φ = 83.110... °, der Dozent gibt Phasenverschiebung φ = 83.35... ° an (vermutlich Rundungs-Effekte). Der Betrag stimmt genau überein.

[ Diese Nachricht wurde geändert von: xeraniad am  9 Sep 2010 15:45 ]

Zu der Brückenaufgabe hatte ich für den Fall "Übertragungsfunktion bei Omega = 1" der Wert 0 angegeben, was nur für n = 2 gilt. Allgemein ist für "Omega = 1" richtig: "A = 1/(n+1) -1/3".

Die Wien-Robinson Brücke werde ich mir morgen nochmal zu Gemüte führen, danke schonmal soweit.

Nun hakts gerade bei dieser Aufgabe:
Bild eingefügt

Die ist ja sehr ähnlich der letzten Aufgabe, daher schnell mein Ansatz:

Zunächst habe ich Z_gesamt berechnet:

Z_gesamt = [(R₂ +X_C2) R₁] / [R₂+X_c2+R₁] = 320,42 - j 21,64 Ohm
Davon dann den Betrag gebildet: 321,15 Ohm

I = U/R --> 31,14 mA

Dann mit der Spannungsteilerformel:

I₁ = (Z_R2,Xc2/R₁) * I₂
...
I₂= 21,155 mA
I₁= 10 mA

Wenn ich nun die Teilspannungen mit dem ohmschen Gesetz berechne ergibt sich für U_R2 9,94 V und für U_Xc2 0,99 V.
Also addiert über 10 V. Müssten nicht an jedem Zweig der Parallelschaltung ganz normal exakt 10 V abfallen?

Bei komplexer Addition kommt wieder U raus, s. Diagramm.
Hier noch die Korrektur zur Wien-Robinson Brücke.

So, endlich bin ich dazu gekommen, deine Lösung der Wien-Robinson Brücke durch zu arbeiten. Das ist alles wirklich sehr verständlich, nur bekomme ich ein leicht anderes Endergebnis:

Wenn man n=2 einsetzt und die beiden Brüche zusammenfasst bleibt durch Kürzen der beiden 3en in Zähler und Nenner im Zähler eine 1 stehen, sodass der Nenner letzlich bei mir j(wrc - 1/wrc) -1 heißt.

Vorsicht, die 3 im Nenner geht nicht weg
A = ⅓ -1÷(j·ω·R·C +3 +1÷{j·ω·R·C}) = j·(ω·R·C -1÷{ω·R·C}) ÷[9 +3·j·(ω·R·C -1÷{ω·R·C})], die Musterlösung ist schon richtig

Ah ok, hatte mich schon gewundert.
Ich habe jetzt die Musterlösung für die Übertragungsfunktion des Bandpasses in den Händen. Mein Prof. hat das sehr einfach gemacht:

Z1 = R + 1/jwc [Reihen-Teil]
Z2 = 1/[1/R + jwc] [Parallel-Teil]

Davon dann den Bruch gebildet und in 2 Schritten aufgelöst.
Meine Frage: Muss Z2 nicht 1/[1/R + 1/jwc] lauten? Ich bin verwirrt...

EDIT: Bin drauf gekommen, es muss ja 1/[1/R + 1/1/jwc] lauten und dann kürzt sich das raus.

[ Diese Nachricht wurde geändert von: Hoover am 13 Sep 2010 16:09 ]

Mir ist nicht klar, wie ich aus der Übertragunsfunktion ein Bode-Diagramm zeichnen kann.
Bei der Wien-Robinson-Brücke lautet A ja


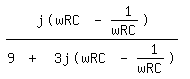
Nun muss ich davon also zunächst den Betrag bilden und die Phasenverschiebung ermitteln.
Wie genau bilde ich den Betrag?


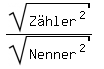
So? Also in diesem Fall:


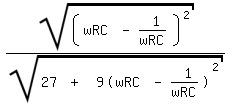
[ Diese Nachricht wurde geändert von: Hoover am 13 Sep 2010 17:36 ]

[ Diese Nachricht wurde geändert von: Hoover am 13 Sep 2010 17:38 ]

Richtig mit Ausnahme der 27.
Betrag |A| der Übertragungsfunktion A = j·(ω·R·C -1÷{ω·R·C}) ÷[9 +3·j·(ω·R·C -1÷{ω·R·C})] der Wien-Robinson-Brücke:
Zähler: Wurzel und Quadrat heben sich auf, daher wird der Zähler ω·R·C -1÷{ω·R·C}.
Nenner: Wurzel aus Summe von Realteil-Quadrat (9² = 81) und Imaginärteil-Quadrat (3³·[ω·R·C -1÷{ω·R·C}]²).
--
Für die Phase φ = atan[Im(A)÷Re(A)] werden zunächst Real -und Imaginärteil benötigt.
An dieser Stelle ist es wünschenswert, A in eine Form mit reellem Nenner zu bringen.
Zu diesem Zweck kann der Bruch mit seinem konjugiert komplexen Nenner erweitert werden.
A = [3·(ω·R·C -1÷{ω·R·C})² +9·j·(ω·R·C -1÷{ω·R·C})] ÷ [9² +3²·(ω·R·C -1÷{ω·R·C})²]
→Re(A) = 3·(ω·R·C -1÷{ω·R·C})² ÷ [9² +3²·(ω·R·C -1÷{ω·R·C})²],
Im(A) = 9· (ω·R·C -1÷{ω·R·C}) ÷ [9² +3²·(ω·R·C -1÷{ω·R·C})²];
Im(A)÷Re(A) = 3÷(ω·R·C -1÷{ω·R·C})
→φ = atan[3÷(ω·R·C -1÷{ω·R·C})]

[ Diese Nachricht wurde geändert von: xeraniad am 14 Sep 2010  9:32 ]

Hier ist noch eine Art Bodediagramm zur Übertragungsfunktion der Wien-Robinson-Brücke. Auf der x-Achse läuft hier die normierte Kreisfrequenz ω·R·C.
gnuplot>
A(W) = 1/3.-1/({0,1}*W+3+1/({0,1}*W))
set xrange [0:12]
set samples 1024
set terminal png
set output 'wr.png'
plot abs(A(x)), arg(A(x))
unset output
Es ist zu erkennen, wie die Phasenverschiebung beim Übergang von ω·R·C < 1 nach 1 < ω·R·C von -½·π nach ½·π springt.

Ah, mit dem komplex konjugierten Nenner erweitern heißt also einfach die Regel für die Division komplexer Zahlen anzuwenden. DU solltest bei uns die Vorlesungen halten.

Ich bin jetzt in das Thema Dioden eingestiegen und die Aufgaben klappen auch alle recht gut. Nur bei dieser Aufgabe bin ich nicht sicher, ob meine Lösung stimmt:

Bild eingefügt

Meine Lösung:

Bild eingefügt

Meine Überlegungen:

1) 0V: kein Strom

2) 1V: An der ersten Diode fallen 0,7 V ab. Da auch die dritte Diode leitet muss reicht die Spannung nicht --> Auch hier 0V

3) 2V: An Diode 1 und 3 fallen zusammen 1,4 V ab. Also bleiben 0,6 V für die restlichen Lasten über. Diode 2 sperrt daher. Nun kann man die 3 Widerstände in Reihe betrachten: An R₂ und R₃ fallen jeweils 0,15 V ab und an R₁ 0,30 V. U_a ist damit = 0,15 V

4) 3V: 3 Dioden leiten, es bleiben also 0,9V über. Damit ist U_a = 0,45V

4) 4V: Siehe oben, U_a = 0,95V

5) 5V: Siehe oben, Ua= 1,45V

Sind meine Überlegungen korrekt?

also bis 1,4 Volt passiert überhaupt nichts (2*0,7V)
ab da hast du einen Spannungsteiler.
ab 2.1 Volt existiert R1 nicht mehr
Gruß Bernd

_________________
Tippfehler sind vom Umtausch ausgeschlossen.
Arbeiten an Verteilern gehören in fachkundige Hände!
Sei Dir immer bewusst, dass von Deiner Arbeit das Leben und die Gesundheit anderer abhängen!