Hier die nächste Aufgabe, an der ich verzweifele:

Bild eingefügt

Folgende Gleichungen habe ich aufgestellt:

U_L = U₂
I₁ = I₂ + 2mA
1200 Ohm = U₁/I₁
470 Ohm = U_l/I₂
R_L = U_L/2mA
U_L + U₁ = 15V

Nun weiß ich nicht, wie ich das Gleichungssystem lösen kann. Das sind für meinen Geschmack deutlich zu viele unbekannte Variablen. Meine Versuche scheiterten bislang...

[Ohne Gewähr, dass dies der effizienteste Weg sei.]
Zunächst nur nach den Strömen auflösen, dann Rl aus I₁ bestimmen.
Knoten mitte rechts: I₁ - I₂ - Il = 0 A
Masche links: R₁·I₁ + R₂·I₂ = Uq
Masche rechts: R₂·I₂ - Rl·Il = 0 V
Das lineare Gleichungssystem mit 3 Gleichungen nach den 3 Unbekannten I₁, I₂ und Il auflösen.
I₁ = Uq·(Rl+R₂)÷(R₁·Rl+R₂·Rl+R₁·R₂) [1],
I₂ = Uq· Rl ÷(R₁·Rl+R₂·Rl+R₁·R₂) [2] und
Il = Uq· R₂ ÷(R₁·Rl+R₂·Rl+R₁·R₂) [3].
Für die erste Teilaufgabe Il nach Rl auflösen.
a) [3] → Rl = R₂·(Uq÷Il -R₁)÷(R₁+R₂) ≈ 1773.05... Ω
b) Ul = Rl·Il = R₂·(Uq -R₁·Il)÷(R₁+R₂) ≈ 3.5461... V
Für die dritte Teilaufgabe den Ausdruck für Il in den für I₁ einsetzen.
c) [1] → I₁ = (Uq+R₂·Il)÷(R₁+R₂) ≈ 9.5449... mA

[ Diese Nachricht wurde geändert von: xeraniad am  6 Sep 2010 17:49 ]

Hier ist noch ein möglicherweise besser nachvollziehbarer Weg. Es sollen nur so viele Unbekannte wie erforderlich verwendet werden.
Hier sind R_L und I₁ gesucht; U_L = R_L·I_L kann später einfach berechnet werden. Anstelle U_L soll zunächst I₂ als gesucht gelten.
Es werden wieder die Knotengleichung und die beiden Maschengleichungen hingeschrieben.
I₁ = I₂ + I_L [1] (Knoten rechts)
R₁·I₁ + R₂·I₂ = U_Q [2] (Masche links)
R₂·I₂ = R_L·I_L [3] (Masche rechts)
Weil nicht nach I₂ gefragt wurde, soll I₂ gleich eliminiert werden: [1] wird nach I₂ aufgelöst und der entstehende Ausdruck in [2] und [3] für I₂ eingesetzt.
[1] → I₂ = I₁ - I_L
(R₁+R_2)·I₁ = U_Q +R₂·I_L [2]
R₂·I₁ = (R_L+R₂)·I_L [3]
Die neue Gleichung [2] kann nach I₁ aufgelöst werden. Diese ist glücklicherweise von R_L unabhängig und damit gleich als Lösung für Teilaufgabe c) geeignet.
[2] → I₁ = (U_Q +R₂·I_L)÷(R₁+R₂) [c]
Der Ausdruck für I₁ wird bei Gleichung [3] eingesetzt. Die Gleichung [3] wird vereinfacht und nach R_L aufgelöst.
R₂·U_Q -R₁·R₂·I_L = R_L·(R₁+R₂)·I_L [3]
[3] → R_L = R₂·(U_Q÷I_L -R₁)÷(R₁+R₂) [a]
Damit kann auch die Lösung für Teilaufgabe b) gegeben werden.
U_L = R_L·I_L = R₂·(U_Q -R₁·I_L)÷(R₁+R₂) [b]

@ xeraniad:
Danke für deine sehr ausführliche und verständliche Hilfe. So konnte ich das Schritt für Schritt nachrechnen und lösen. Klasse.
Bei solchen Aufgaben weiß ich meist einfach nicht, wie ich anfangen soll. Eigentlich hat es nur am ersten Schritt gehapert, als ich I₁ hatte ging der Rest dann ohne Probleme.

Ich hänge an der nächsten Aufgabe, diesmal versuche ich vergeblich eine Übertragungsfunktion eines Bandpasses zu erstellen.

Bild eingefügt

A = U_A/U_E

Nun habe ich die Gleichungen aufgestellt:
Der Widerstand des untereren parallelen Astes sollte wie folgt sein:

1/R_parallel = 1/R + 1/X_c = 1/R + 1/1/jwc

Der Gesamtwiderstand sollte wie folgt sein:

R_ges= R + 1/jwc + R_parallel

Also A = R_parallel/R_ges

Und dann weiß ich nicht weiter. Wenn man diesen Buch bildet entsteht ein Riesenbruch mit ineinander geschalteten Einzelbrüchen.
Wie kommt man von dort auf das Endergebnis? Da muss ich auch sagen, dass ich mit den komplexen Zahlen nicht so fit bin und nicht sicher weiß, wie ich da vereinfachen kann.
Aber der Ansatz stimmt, oder?

Das schreit ja förmlich nach Elektrotechnik Ende zweites Semester

---
Also: du rechnest hier ja mit komplexen Widerständen. Daher ist alles, was nicht rein ohmsch ist, eine Impedanz und wird folglich mit Z und nicht mit R beschrieben.
Da nur zu den Formelzeichen.


Also, die Übertragungsfunktion gibt das Verhältnis zwischen Ausgangsspannung zur Eingangspannung an, also A = Ua/Ue.

Tu so, als sei das alles ein (komplexer) Spannungsteiler. Dort wird ja ebenfalls beschrieben, wie sich die Spannungen und Teilspannungen zu Gesamt- und Teilwiderständen verhalten.
Danach musst du noch ein paar algebraische Tricks anwenden und du hast das Ergebnis wie in der Lösung.

Dein Ansatz für Z_parallel ist richtig, kann aber noch ein wenig umgeformt werden. R || Z_C = R*Z_C/(R+Z_C) = (R*1/(jωC))/(R+1/(j*ωC)) und dann weiter umformen.

_________________


[ Diese Nachricht wurde geändert von: DonComi am  7 Sep 2010 20:55 ]

Nein, ich studiere nicht Elektrotechnik, sondern Bio- und Nanotechnologien und frage mich gerade täglich, warum wir den ganzen Kram überhaupt so ausführlich in unseren Studiengang haben.
Die anderen "Leidensgefährten" sind zum Teil Informatiker und zum Teil Mechatroniker und ein nicht unerheblicher Teil meiner Komilitionen wird im dritten Versuch schreiben (Notenschnitt letztes Mal: 4,5).

Ich habe gerade lang gerätselt, wie du das umgeformt hast, dabei ist es ja einfach nur Bruchrechnung. Manchmal sieht man den Wald vor lauter Bäumen nicht. Mal sehen ob ich jetzt weiter komme.

Mit den Formelzeichen sollte ich mich wirklich mal umgewöhnen, kommt in der Klausur vermutlich nicht so gut an.

EDIT:
Das ist verwirrend...
Ich habe gerade diesen link gefunden, in dem die Aufgabe gelöst und hergeleitet wird. Das Ergebnis ist auch das von meinem Prof. angegebene.

http://www.elektroniktutor.de/analog/rc_pass.html

Nur ist hier die Schaltung anders aufgebaut:

Bild eingefügt

Hier sind im Gegensatz zu meiner Aufgabenstellung die beiden Kondensatoren parallel und nicht in Reihe geschaltet.
Wieso kommt da trotzdem das gleiche raus?

[ Diese Nachricht wurde geändert von: Hoover am  7 Sep 2010 23:53 ]

So, ich habe die Lösung in dem link Schritt für Schritt nachvollzogen/gerechnet und sie mehr oder weniger verstanden. Bleibt die Frage offen, warum das gleiche für die Schaltung in meiner Aufgabe gilt. Das will mir nicht einleuchten.

Ja, ich habs nachgerechnet. Alle drei Ketten (die aus der Aufgabe und die beiden aus dem Link) haben die gleiche Übertragungsfunktion A = 1÷a₁₁ (bzw. den gleichen Vierpol-Kettenparameter a₁₁). Dies ist in der Tat bemerkenswert. Es ist aus irgendwelchen Symmetriegründen möglich, dass verschiedene Netzwerk-Strukturen gewisse Eigenschaften gemeinsam haben. Was war eigentlich die Musterlösungs-Antwort zu Frage d) ?
Meine Antwort wäre gewesen: "Wird die dimensionslose Grösse 'ω·R·C' durch deren Reziprokwert '(ω·R·C)⁻¹' ersetzt, ändert nur das Vorzeichen des Imaginärteils der komplexen Übertragungsfunktion A (d. h. A wird komplex konjugiert)."
Kann dies anschaulicher ausgedrückt werden?

[ Diese Nachricht wurde geändert von: xeraniad am  8 Sep 2010 16:54 ]

Ja, ich habs nachgerechnet. Alle drei verschiedenen RC-4er-Ketten (die aus der Aufgabe und die beiden aus dem Link) haben die gleiche Übertragungsfunktion A = 1÷a₁₁ (bzw. den gleichen Vierpol-Kettenparameter a₁₁). Dies ist in der Tat bemerkenswert. Es ist aus irgendwelchen Symmetriegründen möglich, dass verschiedene Netzwerk-Strukturen gewisse Eigenschaften gemeinsam haben. Was war eigentlich die Musterlösungs-Antwort zu Frage d) ?
Meine Antwort wäre gewesen: "Wird die dimensionslose Grösse 'ω·R·C' durch deren Reziprokwert '(ω·R·C)⁻¹' ersetzt, ändert nur das Vorzeichen des Imaginärteils der komplexen Übertragungsfunktion A (d. h. A wird komplex konjugiert)."
Kann dies anschaulicher ausgedrückt werden?

Hm, von der Schaltung in meiner Aufgabe wäre ich aber nie auf die Lösung gekommen. Da muss man ja erstmal einen anderen Ansatz haben.

Zu d) habe ich keine Musterlösung; die schreibt mein Prof. offenbar nur hin, wenn er Lust dazu hat.

Achja, darf ich fragen, wie lange du ca. brauchst, um eine solche Übertragunsfunktion zu berechnen? Ich saß da ziemlich lange dran mit den diversen Umformungen und habe Sorgen, dass ich das in der Klausur nicht schaffen würde...

In der nächsten Aufgabe muss ich die Übertragunsfunktion einer Wien-Robinson-Brücke ermitteln (das kann ja heiter werden).

Bild eingefügt

Folgenden Ansatz habe ich:
Bild eingefügt

Zur Erklärung:
Bild eingefügt

[Ich habe versucht, diesen Bruch mit LateX zwecks Übersichtlichkeit zu erstellen, aber da habe ich mich immer mit den ganzen Klammern verzettelt; ich hoffe es ist auch so erkennbar]

° Für Ketten-Anordnungen wie die zuvor betrachteten RC-Bandpässe können die Vierpol-Kettenmatrizen elementarer Vierpole multipliziert werden.
Gemäss Vierpol-Theorie wird die Spannungs-Übertragungsfunktion 1÷a₁₁. Mit dem Taschenrechner dauerte das etwa 5 min.
° Wenn ich es manuell durchführen müsste, könnte das für solche 4er-RC-Ketten (mit gleichen R und C) 15 min oder länger dauern, d. h. in einer Klausur wäre ich wohl sehr unter Zeitdruck, da ich meine Resultate gerne noch verifiziere.
Aber Übung macht schneller.
° Die Wien-Robinson-Brücke habe ich noch nicht näher betrachtet. Werde sie noch umzeichnen. Werde auch die Musterlösung verifizieren, verschiedene Lösungswege suchen und dann morgen hoffentlich den schnellsten posten. Kann Dir dann auch mitteilen, ob Deine Ansätze korrekt sind.

° Rechts tritt R₁ auf, aber in der Lösung erscheint nur R.
Ist es richtig, hier R₁ = R anzunehmen?

Schönen Abend

Vielen Dank für deine Hilfe, ich weiß das zu schätzen.

Wir dürfen in der Klausur eine beschriebene Seite mitnehmen. Da werde ich mir dann die Übertragungsfunktionen von Band- und Tiefpass notieren; damit es schneller geht im Fall der Fälle.

Zitat :

Rechts tritt R₁ auf, aber in der Lösung erscheint nur R. Ist es richtig, hier R₁ = R anzunehmen?

Nein, vermutlich nicht. Das verkompliziert das Ganze natürlich weiter.

[ Diese Nachricht wurde geändert von: Hoover am  8 Sep 2010 17:53 ]

Und wieder eine neue Frage:

Bild eingefügt

Mein Ansatz:

R_ges = [(R₂ + 1/jwc₂) * R₁]/[R₂ + 1/jwc₂ + R₁] + 1/jwc₁

Nun weiß ich nicht genau, wie ich die ohmschen Widerstände mit den komplexen der Kondensatoren addieren soll. Muss ich da einfach die Formel



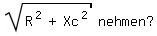
Dann ergeben sich für mich folgende Werte:
- Xc₂ = 1446,86 Ohm
- Xc₁ = 3183 Ohm
- R_gesamt = 3208 Ohm
- I = 15,59 mA

Rauskommen sollen 15,2 mA und nun weiß ich nicht, ob das Rundungsfehler sind, oder ob ich falsch gerechnet habe.

PS: Bin ich blind oder gibts in diesem Formeleditor hier keinen ganz normalen Bruch?

[ Diese Nachricht wurde geändert von: Hoover am  8 Sep 2010 20:46 ]