Hallo,

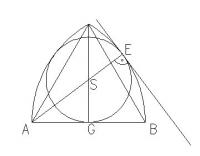
kann mir jemand sagen, wie man in dieser zeichnung den radius des großen Inkreises oder den Radius der kleinen (weißen) kreise in abhängikeit von a ausdrücken kann (es muss begründbar sein)?

die eigentliche aufgabe ist, die grüne fläche in abhängigkeit von a zu berechnen, aber es scheitert an dem radius der kleinen kreise. wenn ich den radius des großen kreises hätte, würde ich den der kleinen kreise berechnen können.

Bild eingefügt

vielleicht nicht gut erkennbar: von links unten bis rechts unten sind 2a

Danke schonmal, Mufti

[ Diese Nachricht wurde geändert von: Mufti am  6 Nov 2004 18:31 ]

Es lässt sich ein rechtwinkliges Dreieck (A, S, G) bilden mit den Seiten



a = Strecke AG - Kathede
r = Strecke GS - Kathede (Radius des dargestellten Kreises)
(2a-r) = Strecke AS - Hypothenuse

Dabei ist vorauszusetzen, daß die Punkte A, S und E auf einer Geraden liegen (beide Linien befinden sich auf dem jeweiligen Berührungsradius zur eingezeichneten Tangente).

Nach Umstellen des Ansatzes



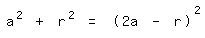
erhält man das Ergebnis:

r = 3/4 a

Beste Grüsse

Jeff

Das heisst sogar: Wenn a 4 Längeneinheiten sind, hat das von mir zum Ansatz gebrachte rechtwinklige Dreieck sogar die "klassischen 3-4-5" als Seitenlänge.

WOW, danke für die schnelle lösung, jeff... des sin halt einfach so sachen die mer erkennen muss, da hab ich immer meine probleme mit....

nochma danke, Mufti

so, ich hab dann mal die grüne fläche ausgerechnet und das hab ich raus...
Gruß, Mufti

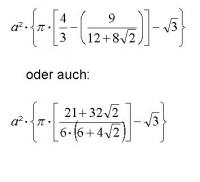
Ja, ich habe es letztlich auch so. Bin auf den oberen Term gekommen. Hatte selbst in meiner Rechnung einen Fehler in der Beziehung -Verhältnis großer Kreis zu den kleinen Kreisen-. Nun ist aber alles auch so wie Du geschrieben hast. Die Probe ergab: Es ist korrekt.