Allpass - Übertragungsfunktion

Allpass - Übertragungsfunktion
Im Unterforum Grundlagen - Beschreibung: Grundlagen und Fragen für Einsteiger in der Elektronik

Nicht eingeloggt Einloggen Registrieren

[Registrieren] -- [FAQ] -- [ Einen Link auf Ihrer Homepage zum Forum] -- [ Themen kostenlos per RSS in ihre Homepage einbauen] -- [Einloggen]

Serverzeit: 01 10 2024 13:28:39 TV VCR Aufnahme TFT CRT-Monitor Netzteile LED-FAQ Osziloskop-Schirmbilder

Elektronik- und Elektroforum Forum Index >> Grundlagen Grundlagen : Grundlagen und Fragen für Einsteiger in der Elektronik

Autor

Allpass - Übertragungsfunktion

Ersatzteilshop für Haushaltsgeräte und Elektronik

BID = 845926

timschmi

Gerade angekommen

Beiträge: 5

Hallo,

ich hoffe ihr könnt mir bei einem kleinen Problem helfen.

Bei folgender Aufgabe komme ich einfach nicht auf die Übertragungsfunktion.

Mein Ansatz:

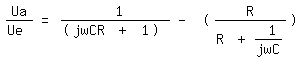
$\fed\mixonUa/Ue = 1/(jwCR + 1) - (R/(R + 1/jwC))$

Und meine Lösung:

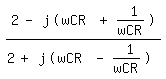
$\fed\mixon(2-j(wCR + 1/(wCR)))/(2+j(wCR - 1/(wCR))$

Selbst wenn ich den Nenner reell mache komme ich nicht auf die Lösung, die angegeben ist. Habe ich schon einen Fehler im Ansatz?

BID = 845934

DonComi

Inventar

Beiträge: 8605
Wohnort: Amerika

Moin, bildet man einen Maschenumlauf z.B. der unteren Masche erhält man ja

U_A=U_C-U_R.
Setzt man nun für beide Spannungen über R und C die Ausdrücke des komplexen Spannungsteilers ein, klammert U_E aus und dividiert die gesamte Gleichung dadurch, erhält man den Ausdruck:
U_A/U_E=(-j/(ωC))/(R-j/(ωC))-R/(R-j/(ωC)).

Das ist der Ansatz, der Rest ist Formelgeschubse.

b) ist ähnlich einfach, ich habe das statt mit Z_c=1/(jωC) mit Z_C=1/(sC) gerechnet und dann, nach ein paar Brucherweiterungen, sieht man schon, dass Zähler gleich Nenner ist und damit die Übertragungsfunktion gerade zu 1 wird (Nenner-/Zählerausdruck ist RCs+1).

_________________

BID = 845943

timschmi

Gerade angekommen

Beiträge: 5

Kann es sein, dass ich UR richtig hatte bei meinem Ansatz und bei UC der Fehler im Nenner liegt?

Der Ansatz müsste doch gleich sein mit deinem?

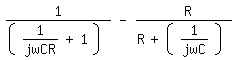
$\fed\mixon1/(1/(jwCR)+1) - R/(R+(1/(jwC))$

BID = 845944

DonComi

Inventar

Beiträge: 8605
Wohnort: Amerika

Moin,

du hast den Fehler im Nenner von U_C;
nach dem Erweitern mit jωC und anschließendem Kürzen mit dem Bruch im Nenner komme ich auf

1/(1+jωRC)

_________________

[ Diese Nachricht wurde geändert von: DonComi am 1 Sep 2012 21:45 ]

BID = 846002

timschmi

Gerade angekommen

Beiträge: 5

Hm dann wäre doch mein Ansatz im 1. Post komplett richtig oder?

BID = 846008

Offroad GTI

Urgestein

Beiträge: 12716
Wohnort: Cottbus

Ja, dein Ansatz ist richtig. Deine Lösung aber nicht. Es ist auch keine richtige Lösung, weil der Nenner immer noch komplex ist, er muss aber reel sein.

Heraus kommt dann:
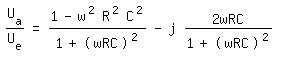
$\fed\mixonU_a/U_e=(1-w^2 R^2 C^2)/(1+(wRC)^2)-j 2wRC/(1+(wRC)^2)$

Edit: Sehe gerade, dass die Lösung ja schon da steht

Werde dir nachher mal den Rechenweg zeigen...

_________________
Theoretisch gibt es zwischen Theorie und Praxis keinen Unterschied. Praktisch gibt es ihn aber.

[ Diese Nachricht wurde geändert von: Offroad GTI am 2 Sep 2012 14:36 ]

BID = 846017

DonComi

Inventar

Beiträge: 8605
Wohnort: Amerika

Wieso?
Ich hätte den Lösungsweg auch hier (eingescannt), aber er soll es selber rechnen!

Der Lösungsansatz ist auch richtig, nur geht es doch jetzt er los: auf den selber Nenner bringen, komplex-konjugiert erweitern ("Nenner reell machen") usw. Das ist nicht schwer.

_________________

BID = 846055

Offroad GTI

Urgestein

Beiträge: 12716
Wohnort: Cottbus

Hast recht, so schwer ist es auch wieder nicht. Dann warten wir mal ab, was uns Tim vorschlägt.

Nur ein kleiner Hinweis für die Lösung: binomische Gleichungen

Offtopic :

sehe gerade, dass ich vorhin ein l unterschlagen habe

_________________
Theoretisch gibt es zwischen Theorie und Praxis keinen Unterschied. Praktisch gibt es ihn aber.

BID = 847062

timschmi

Gerade angekommen

Beiträge: 5

Hatte mich jetzt wieder an der Aufgabe versucht aber ohne Erfolg. Ich lande immer bei meinem Ergebnis :/

Denke bis dahin ist es richtig?

A\fed\mixonA = 1/(1+jwCR) - 1/(1-j/wCR)

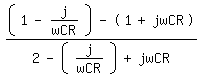
$\fed\mixon((1-j/wCR)-(1+jwCR))/(2-(j/wCR)+jwCR)$

So dann fasse ich zusammen:

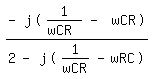
$\fed\mixon(-j(1/wCR - wCR))/(2-j(1/wCR-wRC))$

und mache den Nenner komplex mit:

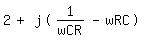
$\fed\mixon2+j(1/wCR-wRC)$

Aber das bringt mich nicht auf das Ergebnis?

BID = 847063

DonComi

Inventar

Beiträge: 8605
Wohnort: Amerika

Du sollst den Nenner reell machen!
Also mit dem Komplex-konjugierten Term erweitern, dann hast du im Nenner nur noch einen Ausdruck der Form

$a^b+b^2$

und im Zähler musst du ausmultiplizieren.
Edit:

_________________

[ Diese Nachricht wurde geändert von: DonComi am 8 Sep 2012 21:56 ]

BID = 847065

DonComi

Inventar

Beiträge: 8605
Wohnort: Amerika

Also:

Spannungsteiler in Maschengleichung einsetzen:
$<br>A(j\omega) = \frac{ \frac{1}{j\omega C}}{\frac{1}{j\omega C}+R} - \frac{R}{\frac{1}{j\omega C} +R}$

Nun im Nenner die Brüche wieder auf denselben Nenner bringen, also R passend erweitern:

$\Rightarrow A(j\omega) = \frac{\frac{1}{j\omega C}}{\frac{1+j\omega RC}{j\omega C}} - \frac{R}{\frac{1+j\omega RC}{j\omega C}} = \frac{1}{1+j\omega RC} - \frac{j\omega RC}{1+j\omega RC}$

So, selber Nenner, also alles auf einen Bruchstrich:

$\Rightarrow A(j\omega) = \frac{1-j\omega RC}{1+j\omega RC}$

Jetzt den Nenner reell machen (Edit: naja, ist eh fast fertig...):

$\Rightarrow A(j\omega) = \frac{1-j\omega RC}{1+j\omega RC} \cdot \frac{1-j\omega RC}{1-j\omega RC} = \frac{1-j\omega RC - j\omega RC - (\omega RC)^2}{1+(\omega RC)^2}$

Nun den Zähler ein wenig aufräumen und fertig:
$\Rightarrow A(j\omega) = \frac{1-(\omega RC)^2}{1+(\omega RC)^2} - j\frac{2\omega RC}{1+(\omega RC)^2}$

Alles paletti?

_________________

[ Diese Nachricht wurde geändert von: DonComi am 8 Sep 2012 22:11 ]

BID = 847068

timschmi

Gerade angekommen

Beiträge: 5

Edit: Oh vielen Dank:)

Ja ich meinte den Nenner reell machen mit der angegebenen Gleichung

Hm mein Ansatz muss falsch sein...

Mein Ergebnis ist:

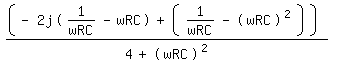
$\fed\mixon(-2j(1/wRC-wRC)+(1/wRC-(wRC)^2)) /(4+(wRC)^2)$

[ Diese Nachricht wurde geändert von: timschmi am 8 Sep 2012 22:25 ]

BID = 847074

DonComi

Inventar

Beiträge: 8605
Wohnort: Amerika

Also im ersten Post war dein Ansatz richtig, danach musst du irgendeinen Fehler gemacht haben, den ich zu suchen jetzt zu faul bin.

_________________

BID = 847075

Offroad GTI

Urgestein

Beiträge: 12716
Wohnort: Cottbus

...hatte da ja auch schon mal was vorbereitet.
Ist im Grunde das, was DonComi schon geschrieben hat, mit der Ergänzung des Betrages.
Die Berechnung des Arguments habe ich jetzt mal weggelassen, weil das ja auch nur phi=arctan(Im/Re)=Zähler(Im)/Zähler(Re) ist. Dass kann man jetzt umstellen, bis man schwarz wird, richtig schön wird der Ausdruck aber nie.

PDF anzeigen

[ Diese Nachricht wurde geändert von: Offroad GTI am 8 Sep 2012 23:27 ]

BID = 847077

DonComi

Inventar

Beiträge: 8605
Wohnort: Amerika

Wobei ich beim Betragbilden den Nenner² aus der Wurzel gezogen habe und dann den Wurzelausdruck ausmultipliziert habe.
Wenn man genau auf den entstehenden Ausdruck

$1 + 2(\omega RC)^2 + (\omega RC)^4$

blickt, sieht man, dass das die Lösung einer Formel vom Typ der ersten Binomischen Formel ist. Man kann es also in ein Quadrat zurückrechnen, die Wurzel ziehen und dann mit dem Nenner vor der Wurzel direkt zu 1 wegkürzen

.

Oder, wie oben kurz angedeutet, man berechnet die allgemeine Übertragungsfunktion mit s statt jω, dann fällt sowieso gleich alles weg.

_________________

Zurück zur Seite 1 im Unterforum Vorheriges Thema Nächstes Thema

Zum Ersatzteileshop

Bezeichnungen von Produkten, Abbildungen und Logos , die in diesem Forum oder im Shop verwendet werden, sind Eigentum des entsprechenden Herstellers oder Besitzers. Diese dienen lediglich zur Identifikation!

Impressum       Datenschutz       Copyright © Baldur Brock Fernsehtechnik und Versand Ersatzteile in Heilbronn Deutschland

gerechnet auf die letzten 30 Tage haben wir 18 Beiträge im Durchschnitt pro Tag       heute wurden bisher 10 Beiträge verfasst
© x sparkkelsputz        Besucher : 182105683   Heute : 2171    Gestern : 5799    Online : 466        1.10.2024    13:28
4 Besucher in den letzten 60 Sekunden        alle 15.00 Sekunden ein neuer Besucher ---- logout ----viewtopic ---- logout ----

xcvb ycvb

0.0367481708527