| Autor |
|
|
|
BID = 653410
DonComi
Inventar
     

Beiträge: 8605
Wohnort: Amerika
|
|
Moin Jungs!
Wie ihr vielleicht mitbekommen habt, habe ich mich gezwungener Maßen ein wenig aus dem Forum zurückgezogen. Meine Aktivität wird sich wohl auf das beschränken, was mir vom Wochenende bleibt  ... ...
Nun hätte ich eine Frage an die Mathegenies unter euch (ja, es ist eine Übung und ja, ich habe selbst schon lange dran gesessen):
Gegeben sei (durch eine lange vorherige Umformung)
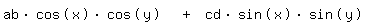
Nun hatte ich mir schlau gedacht, dass mit den Additionstheoremen zusammenzufassen, was ohne die Koeffizienten kein Problem wäre.
Ausklammern und den Kehrwert der Koeffizienten bilden würde mich auch nicht weiter bringen  ... ...
Ist es also möglich, das Additionstheorem anzuwenden, und wenn ja, wo landen die Koeffiziente a,b,c und d?
Ihr würdet mir sehr helfen, auch wenn ich zur Not eine eher spezielle Lösung aufschreiben würde (mit Koeffizienten gleich 1  ). ).
Aber das will er wohl nicht sehen...
Hab auch einige Möglichkeiten durchprobiert, aber die Ergebnisse ergaben keine Gleichheit. In meinem Bronstein stehen die Theoreme wie bei Wiki.
http://de.wikipedia.org/wiki/Formel.....oreme
Danke und Gruß,
D.

Edit: oder kann es sein, dass ich den Wald vor lauter Bäumen nicht sehe? Soll ja vorkommen, wenn man lange genug dransitzt..
_________________
[ Diese Nachricht wurde geändert von: DonComi am 7 Dez 2009 20:19 ] |
|
BID = 653424
DonComi
Inventar
     

Beiträge: 8605
Wohnort: Amerika
|
|
---
[ Diese Nachricht wurde geändert von: DonComi am 7 Dez 2009 21:14 ] |
|
BID = 653430
perl
Ehrenmitglied
       

Beiträge: 11110,1
Wohnort: Rheinbach
|
Zitat :
| Gegeben sei (durch eine lange vorherige Umformung)
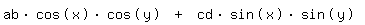
|
1.) Ist die langweilige Umformung, und damit dieser Ausdruck, richtig?
2.) In welche Richtung willst du diesen Ausdruck, eine Gleichung ist es ja nicht, denn umformen?
Formatierung repariert - MfG clembra 
[ Diese Nachricht wurde geändert von: clembra am 7 Dez 2009 21:41 ]
|
BID = 653436
DonComi
Inventar
     

Beiträge: 8605
Wohnort: Amerika
|
Moin perl,
ja, die stimmt.
Es geht darum, zu zeigen, dass das Produkt zweier trigonometrischer Polynome wiederum ein trig. Polynom als Ergebnis liefert.
Das ist mir für den Fall, dass die Koeffizienten 1 sind, ja auch gelungen.
Es soll sowas rauskommen wie:
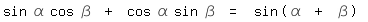
So langweilig ist der ausgeschriebene Ausdruck gar nicht, wenn man zwei trig. Polynom. n-ter Ordnung multipliziert... Edit: naja, doch  .
_________________
[ Diese Nachricht wurde geändert von: DonComi am 7 Dez 2009 21:41 ]
|
BID = 653454
perl
Ehrenmitglied
       

Beiträge: 11110,1
Wohnort: Rheinbach
|
Meinst du folgendes?
Ausdruck = ab* 1/2 *[cos(x-y) + cos(x+y)] + cd* 1/2 *[cos(x-y) - cos(x+y)]
Das brauchst du dann nur noch umzusortieren. 
P.S.:
Das steht auch in deinem Wiki-Link in den ersten zwei Zeilen unterhalb der Überschrift "Produkte der Winkelfunktionen"
[ Diese Nachricht wurde geändert von: perl am 7 Dez 2009 23:16 ]
|
BID = 653475
DonComi
Inventar
     

Beiträge: 8605
Wohnort: Amerika
|
Moin,
und erstmal Danke!
Habe die Lösung gefunden.
Es ging darum, einen Ausdruck, indem acht Winkelfunktionen vorkamen, auf einen Ausdruck mit zwei Winkelfunktionen umzuformen.
Eben dass aus
cos(a)*cos(b)+sin(a)*sin(b) --> cos(a-b)
Allerdings störten mich halt die Faktoren i,k in den Summanden k*cos(a)*cos(b)+i*sin(a)*sin(b).
_________________
[ Diese Nachricht wurde geändert von: DonComi am 7 Dez 2009 23:23 ]
|
BID = 653497
perl
Ehrenmitglied
       

Beiträge: 11110,1
Wohnort: Rheinbach
|
Zitat :
| | Habe die Lösung gefunden. |
Was gab es da noch zu finden?
Der obige Ausdruck enthält nur noch cos(x+y) und cos(x-y).
Die Klammer auszumultiplizieren und die Koeffizienten zusammenzufassen kann jeder Achtklässler; deshalb habe ich mir das gespart.
|
BID = 653506
DonComi
Inventar
     

Beiträge: 8605
Wohnort: Amerika
|
Ebend!
Danke fürs Augenöffnen.
Manchmal sieht man halt den Wald vor lauter Bäumen nicht.
[ Diese Nachricht wurde geändert von: DonComi am 8 Dez 2009 0:30 ]
|




 ...
...


