Vor einiger Zeit habe ich im Chat mal gefragt, wie man aus Drehstrom die Sinus- und Cosinus- Spannungen x und y machen kann, eine Phasenverschiebung von 90° also.
Weil das ist nicht ganz offensichtlich, aber, wie fast immer, am Schluß ganz einfach ist, mußte ich mir die Frage leider wieder einmal selbst beantworten.
Hier also kommt die Lösung.
Aus der Zeigerdarstellung der drei Phasen,
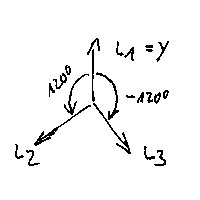
folgen deren Spannungs-Zeitfunktionen:
L1=cos(wt)
L2=cos(wt+120°)
L3=cos(wt-120°)
L1 ist also schon die gewünschte cos Spannung, und wir können sie direkt verwenden: y=L1
Zeichnerisch ergibt sich dann die dazu um 90° verschobene x-Spannung, indem man L2 zunächst um 180° dreht:
Das ist das gleiche wie -L2
und dann -L2 zu L3 vektoriell addiert:
Gewöhnlich nennt man diese Operation eine Subtraktion, und das Ergebnis die Differenz.
Da in dieser Skizze möglicherweise ein Amplitudenfehler steckt, rechnen wir nun nach:
x= L3 + (-L2) = cos(wt-120°) - cos(wt+120°)
Wir suchen das passende Additionstheorem:
cos(alpha +- beta) = cos(alpha)*cos(beta) -+ sin(alpha)*sin(beta)
und erhalten:
x= cos(wt)*cos(120°) + sin(wt)*sin(120°) - cos(wt)*cos(120°) + sin(wt)*sin(120°)
Der erste und der dritte Summand heben sich auf, und damit wird
x= 2* sin(120°)*sin(wt)
Da
sin(120°) = sin(60°) = 1/2 * Wurzel(3),
wird
x= sqr(3)*sin(wt).
Die x-Spannung ist also um das 1,73 fache zu groß.
(Das war ja klar, werden die Elektriker jetzt sagen.)
Somit erhalten wir für die Gesamtschaltung:
Das ist vielleicht nicht die schönste Lösung, aber bestimmt die einfachste um um 90° verschobene phasenstarre Spannungen herzustellen, um z.B Schrittmotore anzutreiben.
_________________
Haftungsausschluß:
Bei obigem Beitrag handelt es sich um meine private Meinung.
Rechtsansprüche dürfen aus deren Anwendung nicht abgeleitet werden.
Besonders VDE0100; VDE0550/0551; VDE0700; VDE0711; VDE0860 beachten !
[ Diese Nachricht wurde geändert von: perl am 31 Mai 2003 0:37 ] 
