| Autor |
|
|
|
BID = 771634
wulf
Schreibmaschine
    

Beiträge: 2246
Wohnort: Bozen
|
|
Hallo,
habe heute ein kleines Matheproblem. Ich sitz grad aufm Schlauch.
Die Lösung ist bestimmt recht einfach aber im Moment gehts nicht.
Folgendes Problem:
Ich möchte diese Formel auflösen.
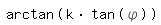
Die Konstante k ist zwar eine riesen Formelwurst, aber nicht von phi abhängig, also hier Konstant.
Die volle Formel würde so lauten:
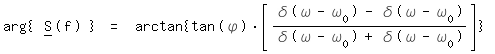
Vielleicht hat jemant eine Idee.
Danke und Grüße
Simon
_________________
Simon
IW3BWH
[ Diese Nachricht wurde geändert von: wulf am 21 Jun 2011 11:58 ] |
|
BID = 771644
Offroad GTI
Urgestein
     

Beiträge: 12798
Wohnort: Cottbus
|
|
Hallo Simon,
könntest du noch ein paar Infos (Anfangsbedingungen/Randbedingungen sofern vorhanden - weil in der fertigen Formel etwas von w0 steht) zu der Formel geben (genau genommen ist es gar keine Formel, weil ein Gleichheitszeichen fehlt).
MfG Mathias |
|
BID = 771645
perl
Ehrenmitglied
       

Beiträge: 11110,1
Wohnort: Rheinbach
|
Zitat :
| | Vielleicht hat jemant eine Idee. |
Das liest sich, als ob 0 rauskäme, da im Zähler 0 steht. 
|
BID = 771649
wulf
Schreibmaschine
    

Beiträge: 2246
Wohnort: Bozen
|
Oh Mann. Hast recht perl, hab mich beim Formeleditor vertippt.
Ich versuchs nochmal:
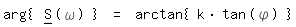
Und die gesamte Formel:
![\fed\mixonarg{ S__(\omega) } = arctan[ ( \delta(\omega-\omega_0) - \delta(\omega+\omega_0) )/(\delta(\omega-\omega_0) + \delta(\omega+\omega_0)) *tan(\phi) ]](fed/mprender.php?stringid=30214)
Die Deltas sind Dirac Deltas und das Omega ist die Kreisfrequenz. Omega 0 ist die Kreisfrequenz der Periode.
Das ganze soll eine Sinusschwingung mit Phase sein und dann Fouriertransformiert. Beim Amplitudenspektrum passt eh alles, nur hier beim Phasenspektrum klemmts noch.
Randbedingungen und Anfangsbedinungen gibts eigentlich keine.
Grüße
Simon
_________________
Simon
IW3BWH
[ Diese Nachricht wurde geändert von: wulf am 21 Jun 2011 14:11 ]
|
BID = 771735
Offroad GTI
Urgestein
     

Beiträge: 12798
Wohnort: Cottbus
|
Da müsste doch eigentlich

rauskommen...is ja schon was später.
MfG Mathias
|
BID = 771747
perl
Ehrenmitglied
       

Beiträge: 11110,1
Wohnort: Rheinbach
|
Zitat :
| Ich möchte diese Formel auflösen.

|
Nach phi oder nach k ?
Beides ist einfach:
y=arctan(k*tan(a))
dann ist
tan(y) =k*tan(a)
und entweder:
tan(a)= tan(y)/k
a= arctan(tan(y)/k) siehe auch die Lösung von Offroad GTI
oder
k= tan(y)/tan(a)
[ Diese Nachricht wurde geändert von: perl am 21 Jun 2011 23:20 ]
|
BID = 771748
DonComi
Inventar
     

Beiträge: 8605
Wohnort: Amerika
|
Ein Tipp vielleicht noch:
CAS-Systeme wie Maxima oder Maple (Derive kanns auch) sind dazu auch in der Lage.
Im Prinzip gilt es bloß die Umkehrfunktion zu benutzen.
Sollte aber eigentlich kein Zauberei für dich sein...
_________________
|
BID = 771751
QuirinO
Schreibmaschine
    

Beiträge: 2205
Wohnort: Behringersdorf
| 
Ich habe nur die Erfahrung gemacht, dass die Benutzung von Maple etc. nicht hilft das Gehirn dabei abzuschalten.
1. wollen die Programme richtig gefüttert werden
2. liefern sie, je nach Problem oft recht komplexe oder unerwünschte Lösungen, die man dann erstmal fachmännisch je nach Problemstellung auswählen muss.. Das Programm rechnet einem ja auch rigoros jede noch so komplexe (no pun intended) Lösung bis zum Schluss durch und spuckt sie einem wortlos aufs Blatt...
|
BID = 771775
DonComi
Inventar
     

Beiträge: 8605
Wohnort: Amerika
|
Hallo,
Wer sowas mit abgeschaltetem Gehirn kann, ist bewundernswert. Speziell hier würde ich auch keine CAS-Systeme benutzen, da die Arkusfunktionen ja recht häufig sind. Wenn es Sachen wie Hyperbelfunktionen sind, dann würde ich wohl eher ein solches System benutzen.
Mal ehrlich, wenn ich einen Ausdruck wie t·sin²(ωt) integrieren will (nacht t), dann nutze ich CAS oder Bronsteins Tabellen. Aber Lust habe ich selten, dann mittels partieller Integration oder Substitution den Kram selbst zu machen. Dafür sind solche Systeme goldwert.
Wie gesagt, der Aufwand muss sich lohnen. Beim Arkustanges hier hätte ich das auch nicht gemacht, war ja auch allgemein.
_________________
|
BID = 771784
wulf
Schreibmaschine
    

Beiträge: 2246
Wohnort: Bozen
|
Auh weh.
Ich habe arg{S} ja gar nicht, das möchte ich ja berechnen.
Am Ende sollte irgendwas in der Richtung
arg{S(w)} = phi*delta(w-w0) - phi*delta(w+w0)
herauskommen.
Das gebieten jedenfalls die Sätze der Fouriertransformation.
Nur wie ich analytisch dahinkommen, b.z.w. hier weiterkomme, weiß ich nicht.
Aber ich werde mal mit der Symbolic Toolbox von Matlab spielen und mich dann wieder melden.
_________________
Simon
IW3BWH
|
BID = 771800
perl
Ehrenmitglied
       

Beiträge: 11110,1
Wohnort: Rheinbach
|
Zitat :
| | Ich habe arg{S} ja gar nicht, das möchte ich ja berechnen. |
Die Formel dafür steht ja eingangs.
Zitat :
| Am Ende sollte irgendwas in der Richtung
arg{S(w)} = phi*delta(w-w0) - phi*delta(w+w0)
herauskommen. |
Also du willst die Formel arctan(k*tan(/)) vereinfachen?
Bin zu faul das zu eruieren, aber ich vermute, daß es über die Identität tan = sin/cos und die Additionstheoreme läuft. Die Eigenschaften von delta() sind mir leider nicht so geläufig.
Warum beschäftigst dich überhaupt mit so perversen Dingen? 
|
BID = 771829
wulf
Schreibmaschine
    

Beiträge: 2246
Wohnort: Bozen
|
Hallo,
ich war heute beim Übertragungstechnikprofessor und er konnte mir (analytisch) auch nicht weiterhelfen.
Er hat gesagt, dass ich mir das so nicht antun soll, da man die Phase ja eigentlich schon vorher "herauslesen" kann.
Ich hatte eben gefragt wie das whol strikt analytisch aussehen würde. Das könnte man ja z.B. bei einer rechnergestützten Implementierung mal brauchen (oder auch nicht, sollte es da auch Tricks geben).
Naja, das (perverse) Thema darf als abgehakt betrachtet werden.
Danke an alle die sich den Kopf zerbrochen haben.
@perl: Ich habe das selbe wie du Vermutet, aber dann auch keine Idee gehabt wie ich das über die Additionstheoreme sinnvoll(!) weiterverarbeiten könnte.
Übrigens hatte ich heute am Morgen die Prüfung in Übertragungstechnik, das war zum Glück dann nicht gefragt. 
_________________
Simon
IW3BWH
|