| Autor |
|
|
|
BID = 384985
M@xxx
Gelegenheitsposter
 
Beiträge: 50
Wohnort: Karlsruhe
|  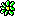
|
Hallo zusammen!
Ich habe eine Frage zur Widerstandsberechnung in folgendem Netzwerk. Alle Widerstände R seien gleich groß.
Ich habe die Schaltung schon vereinfacht, da sie symmetrisch ist. Den Widerstand, auf den der Pfeil zeigt, kann man ja weglassen da an seinen Polen das gleiche Potential herrscht.
Nun weiß ich nicht, wie ich die resultierende Schaltung rechts berechnen kann...
Grüße, Max |
|
BID = 384992
Jornbyte
Moderator
      

Beiträge: 7178
|
|
Der Gesamtwiderstand in einem elektrischen Widerstandsnetzwerk lässt sich mittels einer Zerlegung in elementare Reihen- und Parallelschaltung berechnen. Dabei gilt für den Gesamtwiderstand R
bei Reihenschaltung der Widerstände:
R= R1+ R2+ Rn
bei Parallelschaltung der Widerstände:
1/R = (1/R1) + (1/R2) + (1/Rn)
_________________
mfg Jornbyte
Es handelt sich bei dem Tipp nicht um eine Rechtsverbindliche Auskunft und
wer Tippfehler findet, kann sie behalten. |
|
BID = 384993
abracadabra
Stammposter
   
Avatar auf
fremdem Server !
Hochladen oder
per Mail an Admin
Beiträge: 361
|
Mann kann doch die gesamte Schaltung mittels Stern-Dreieck Umformungen auf einen einzigen Widerstand reduzieren..
Gruß
abracadabra
|
BID = 384996
Brizz
Stammposter
   
Beiträge: 386
Wohnort: Rheine
|
Wie Du von der linken zur rechten Schaltung gekommen bist, weiß ich nicht. Eine Berechnung ist nur mit Stern-Dreieck-Umwandlungen möglich, daher kann man die linke Schaltung nicht vereinfachen.
Wenn man die rechte als gegebene Schaltung betrachtet, ist die aber noch zu vereinfachen.
In der rechten Schaltung liegen doch drei Widerstände parallel, die kannst Du zusammenfassen, dann bleibt eine Parallelschaltung von einem Widerstand und einer Reihenschaltung von zwei Widerständen.
[ Diese Nachricht wurde geändert von: Brizz am 11 Nov 2006 22:05 ]
|
BID = 384999
Jornbyte
Moderator
      

Beiträge: 7178
|
Wenn der Fragesteller seine Zeichnung gegen den Uhrzeigersinn 90° dreht und etwas besser zeichnet, wird alles einfacher.
_________________
mfg Jornbyte
Es handelt sich bei dem Tipp nicht um eine Rechtsverbindliche Auskunft und
wer Tippfehler findet, kann sie behalten.
|
BID = 385025
M@xxx
Gelegenheitsposter
 
Beiträge: 50
Wohnort: Karlsruhe
|  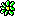
Oh ja,
da sieht man wieder, wie wichtig es ist, Schaltungen sinnvoll umzuzeichnen...
also ist rechts eine Parallelschaltungen aus
einem Widerstand
und
einem Widerstand seriell zur Parallelschaltung von drei Widerständen.
Wie ich von der linken Seite zur rechten gekommen bin:
In der linken Schaltung gibt es eine Symmetrielinie, die waagerecht durch den mittleren waagerechten Widerstand verläuft. Die Symmetrie ist seriell, d.h. ich muss den Gesamtwiderstand der einen Hälfte mal zwei nehmen, um auf den Gesamtwiderstand der linken Schaltung zu kommen.
Und die Punkte der Schaltung, die die Symmetrielinie schneidet, haben alle gleiches Potenzial, daher kann man den einen waagerechten Widerstand auch weglassen oder überbrücken, da kein Strom durch ihn fließt, bzw. den halben Widerstand rechts mit dem Knoten verbinden.
Max
|
BID = 385033
abracadabra
Stammposter
   
Avatar auf
fremdem Server !
Hochladen oder
per Mail an Admin
Beiträge: 361
|
Mit der Symmetrie hast Du recht.
Du solltest die Bauteile benennen damit es leichter fällt sich über eine Schaltung mit Anderen auszutauschen.
Nun..
Die beiden unteren Widerstände sind parallel, also kannst Du sie zusammenfassen.
Danach musst Du eine Stern-Dreieck Umwandlung vornehmen.
Oder Dreieck-Stern, die erste Variante ist jedoch in dem Fall günstiger.
[ Diese Nachricht wurde geändert von: abracadabra am 11 Nov 2006 23:34 ]
[ Diese Nachricht wurde geändert von: abracadabra am 11 Nov 2006 23:37 ]
|
BID = 385067
Brizz
Stammposter
   
Beiträge: 386
Wohnort: Rheine
|
Mit der Symmetrie hast Du recht.
Also gilt für den Gesamtwiderstand:
Rges = [(R/2 || R || R) + R] || R] * 2
Rges = [(R/4 + R) || R] * 2
Rges = [R/5 || R] * 2
Rges = R/6 * 2
Rges = R/3
|
BID = 385071
Brizz
Stammposter
   
Beiträge: 386
Wohnort: Rheine
|
Da habe ich mich verrechnet.
Also gilt für den Gesamtwiderstand:
Rges = [(R/2 || R || R) + R] || R] * 2
Rges = [(R/4 + R) || R] * 2
Rges = [1,25R || R] * 2
Rges = 5/9 * R * 2
Rges = 10/9 * R
|